测量数据预处理
数据处理
信号调理
放大、滤波、I/V转换
一次处理
系统误差校正、数字滤波,逻辑判断、标度变换
二次处理
前两步得到的测量数据进行分析,寻找规律,判断事物性质,生成所需要的控制信号
系统误差
定义
特点
处理原则
方法
数字调零
全自动校准:既可消除零点漂移和偏移的影响
$$
V=(\frac {x-x_0} {x_1-x_0})\times V_REF
$$人工自动校准
线性化处理
- 查表法
- 数学表达式换算
- 软测量方法
- 折线近似及线性插值
标度变换方法
线性变换公式
公式转换法
$$
V=(\frac {Y_{max}-Y_{min}} {N_{max}-N_{min}})(X-N_{min})+Y_{min}
$$
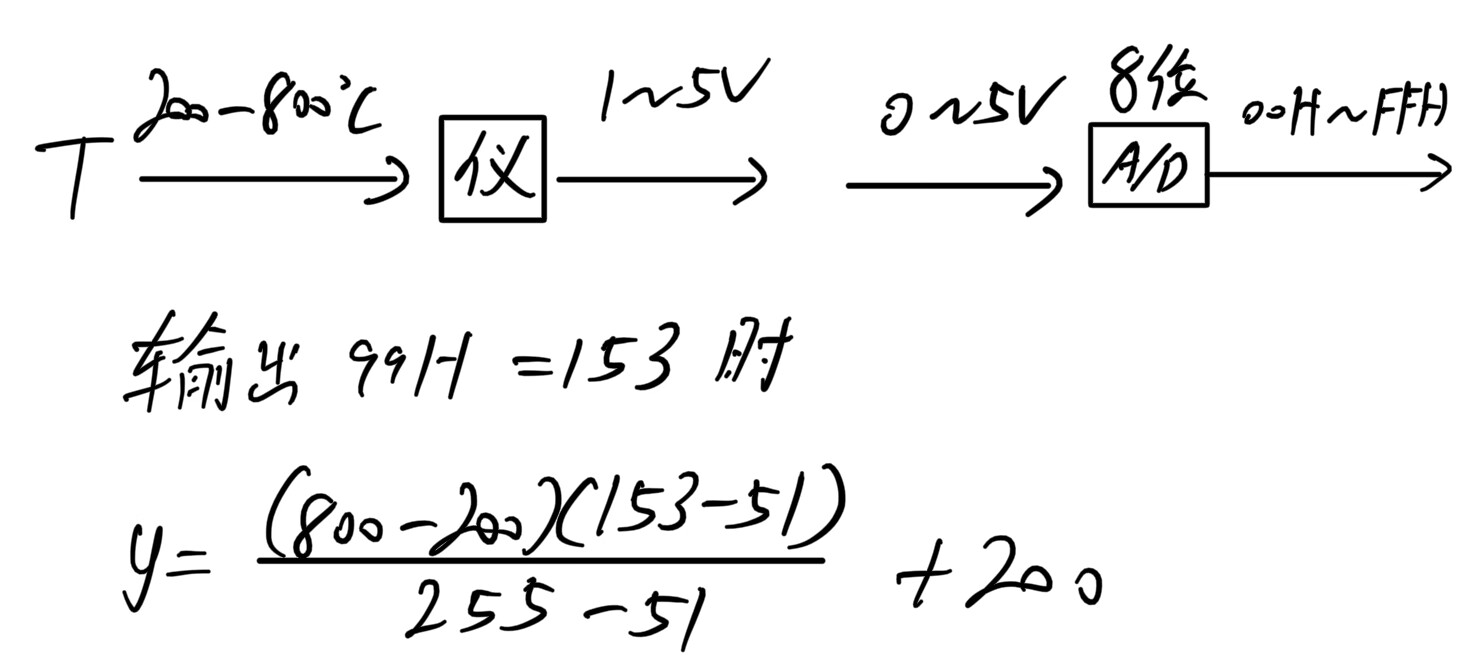
- 其他标度变换法
越线报警处理
量化误差来源
- 量化误差
- 量化单位:$q=\frac 1 {2^{n_1}-1}\approx 2^{-n_1}$
- 余数处理
- 截尾
- 舍入
字长选择与分辨率
分辨率
- $D=\frac 1 {2^{n_1}-1}$
字长
$n\ge \log_{2}{(1+\frac{x_{max}-x_{min} }{\lambda } )} $
$\lambda$的求解需要注意,要转换为对于AD而言单位是$\frac{mv} {bit}$
例如:要从1000°分辨4°,AD输入[0-5V]
$\lambda$=$\frac{4}{1000}×5000$
$n\ge \log_{2}{(1+\frac{5000-0}{\lambda } )} $
$n\ge \log_{2}{(1+\frac{1}{D_{0} } )} $
软件抗干扰技术
噪声
- 周期性
- 随机信号
数字滤波
算术平均值滤波
- 算术平均值法适用于随机干扰信号的滤波
中位值滤波
- 对缓慢变化的过程采用中位值滤波有良好的效果
限幅滤波
- 适用于偶然的大的脉冲干扰或采样器的不稳定,使得采样值偏离实际值太远
惯性滤波法
- 一阶惯性滤波用于高频及低频干扰信号的滤除
递推(滑动)平均滤波法
- 递推平均滤波算法对周期性干扰有良好的抑制作用,平滑度高,灵敏度低
加权递推平均滤波法
- 适用于有较大纯滞后时间常数的对象和采样周期较短的系统
结论:
平均值滤波法适用于周期性干扰
中位值滤波法和限幅滤波法适用于偶然的脉冲干扰
惯性滤波法适用于高频及低频的干扰信号
加权平均值滤波法适用于纯迟延较大的被控制对象